Podcasts and webinars
Rescuing failed subscription payments using contextual multi-armed bandits
By Ralph Myers, Data Scientist, Adyen, and Richard Price, Data Scientist, Adyen

Many businesses incorporate or are built around subscription products, such as Spotify or Apple Music. A common challenge for these businesses is ensuring a successful charge every month. On a small scale, some amount of failed repeating payments is unavoidable, whether due to fraud, an expired card, or even insufficient funds. However, if enough payments suffer this same fate, revenues can falter. This is obviously undesirable, and has clear implications for customer churn and, in extreme cases, the long term viability of a merchant’s business model.
About a year ago we asked ourselves: “What more can we do to help our merchants who face this problem? Our aim was to investigate whether we could build a product that could, using intelligent logic based on the huge amount of payment data in our system, give companies the highest chance of recovering failed recurring payments. Ina previous blogyou might have heard of RevenueAccelerate; the product described here has now gone on to become one of RevenueAccelerate’s main features.
The naive approach
The most common approach to ensuring a successful charge for monthly payments is to retry the payment a certain number of times within a fixed amount of time. Let’s consider an example. Mary’s Wine Club charges a monthly fee in exchange for a selection of premium wines that their customers can try each month. On the 25th of the month, one of their customers has a failed subscription payment. Rather than having to pick up the phone or send an email to the customer, Mary’s Wine Club instead decides to try rescheduling the transaction, and decides to retry 7 times over the next 28 days. If they fail after that period, then they reach out to the customer directly and pause that customer's subscription.
We can break down this approach with two core concepts:
- Remaining retry attempts: the number of outstanding attempts to make for a payment. In Mary's Wine Club example, this starts at 7 retry attempts.
- Retry window: The amount of time after the initial failed payment during which to attempt payments. This was over 28 days in the Mary's Wine Club example.
Now, given a failed subscription payment, what is the optimal way to schedule theremaining retry attemptswithin theretry windowin order to maximize the probability that the failed payment is converted?
Let’s first consider a simple strategy. Putting ourselves in the merchant’s shoes, we could just spread the remaining attempts evenly across the next 28 days. This would mean retrying every four days in the hope that at some point this customer might have enough money in their account, or that whatever other issue facing the payment originally has now been resolved.
Why this isn’t that great
In principle, this seems like a good idea and could go a long way towards helping the payment to convert; however, it is not without its issues. Let’s have a look at what happens when we try to apply this strategy in country X.
Below, we see the expected probability of a successful retry conditional on the day of the month. In some cases, this approach strikes lucky, whereas in other instances this choice is clearly suboptimal.
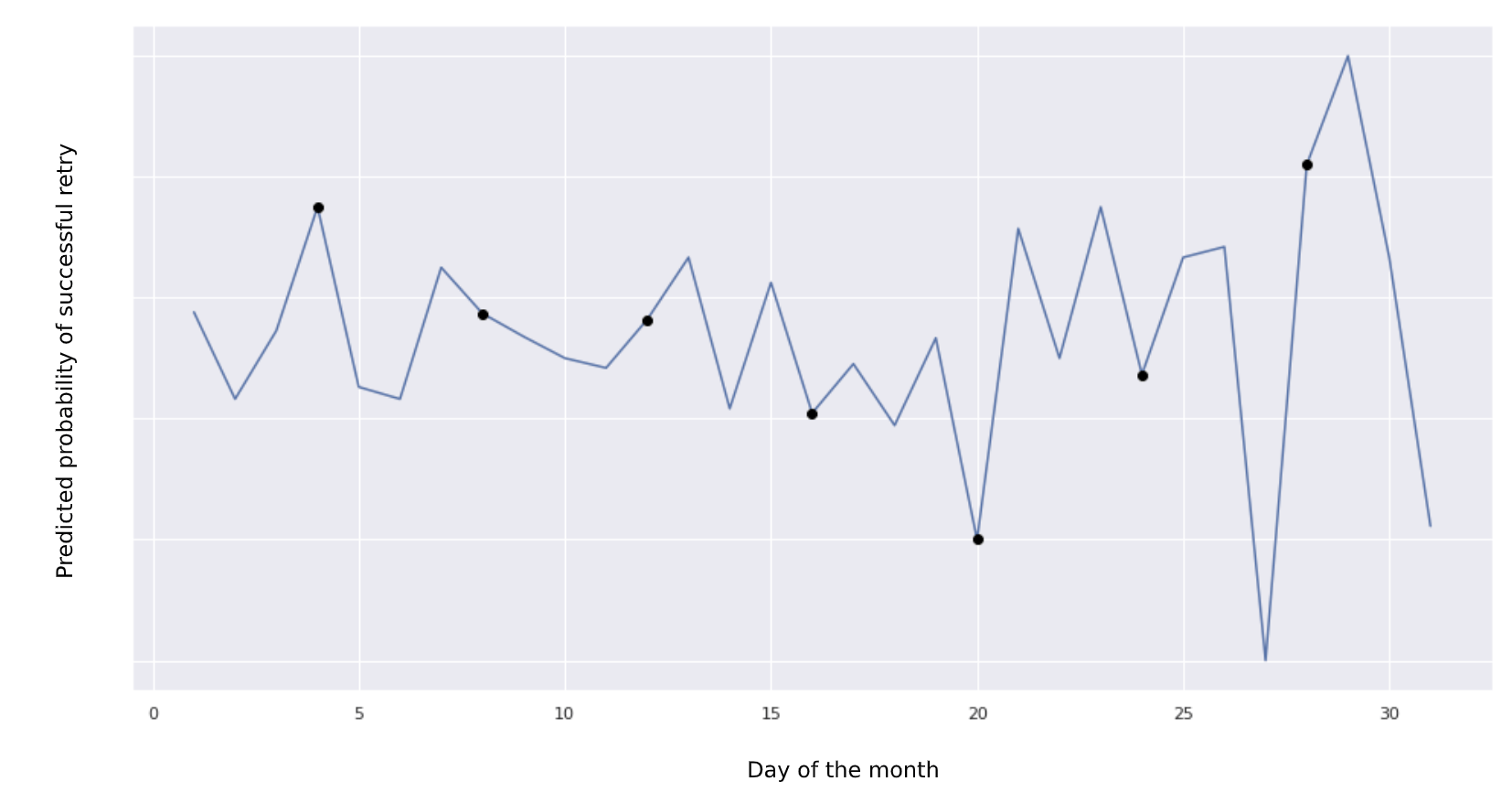
Probability of a successful retry by day of month.
There are many other factors that might influence the outcome of a retry:
- What if the reason the payment failed was simply that there were insufficient funds in the customer’s account? In such an event, waiting until the next payday might be a better strategy.
- What if we can tell when this payday will be based on where the customer is located? Incorporating this information into our scheduling logic would make sense.
- What if we know that at certain peak times, the customer’s issuing bank will randomly reject more payments due to system load, and that once this passes, we can try again almost immediately?
Unfortunately, there are likely to hundreds, if not thousands, of these types of rules that could apply to this particular customer and payment. With this in mind, we need a smarter decision-making system, one that is able to learn as many of these rules as possible to give the best chance of payment conversion.
Along with incorporating more factors to help in this decision making, we also need to ensure that the new decision-making system doesn’t just repeat what seemed optimal at the time; it should also be able to effectively respond to new and changing situations. This system needs to effectively distribute all of the available retries across the retry window, and not put all its eggs in one basket, so to speak.
Our approach
Similar to ourprevious blog postabout optimizing payment conversion rates, we decided to cast this as a contextual multi-armed bandit problem and solve it by implementing a variation on the classic random forest algorithm. Recall that a contextual bandit can be thought of as a repeated game with each stage consisting of the following steps:
- A context (payment characteristics) is produced by the environment and is observed by the player
- The player chooses an action (or arm if we want to stick to the gambling metaphor)
- Some reward is observed by the player
In the case of the AutoRescue model, the action space is considered to be all possible future times at which to retry the failed payment, within the retry window. We accept a trade-off between exploration and exploitation because of:
- Selection bias: previous policies might have oversampled on certain actions whilst leaving others out completely.
- New contexts: we might onboard a new merchant that has most of its payment volume originating from a country for which the model has received few samples to train on.
- Dynamic environment: the learned relationships between contexts and rewards don’t hold over time (e.g. the coronavirus epidemic).
Initial experimentation showed that tree-based classifiers gave the best results and would already generate a significant uplift using an exploitation-only approach. Nevertheless, we wanted to include an element of exploration in our model for the above mentioned reasons and considered a number of approaches in doing so. Ultimately, we decided on an epsilon-greedy approach, but taking into account the degree of confidence of the model predictions during the random action selection stage.
Since random forests showed favorable results during experimentation, we decided to use this algorithm since it relies on bootstrapping, and can therefore provide information about the full conditional distribution of the target variable. Instead of averaging the results of the individual trees in the forest, we can use these predictions to form an empirical distribution from which to sample, thereby emulating the process of Thompson Sampling from a posterior distribution.
Before we continue let’s clarify a few of the terms we just used:
- Epsilon-greedyis a straightforward approach to balancing exploration versus exploitation. During each round we choose the actions that have the highest predicted probability of success at that point in time. For 1-ε of the games we choose a random action. ε is thus a tunable parameter that we can set to any value between 0 and 1. Every time we observe a reward we update our probabilities, meaning the preferred action to choose can switch over time.
- Random forestsare a type of algorithm that aggregate the results of multiple decision trees, which often leads to better results than relying on the estimates of an individual tree. A degree of randomness is introduced to ensure the individual trees don’t all produce the same result. One of the ways in which randomness is introduced is through bootstrapping.
- Bootstrappingmeans sampling with replacement. Each tree in the random forest is trained on a bootstrapped dataset.
- Theconditional distribution of the target variable, as opposed to the conditional (weighted) mean usually returned by the random forest, can be used to infer the degree of confidence with which the model makes predictions for a given action. Thus for actions where there is a strong relationship between the payment characteristics and the probability of a successful retry, that is easily learnt by the decision trees, we expect their predictions to be closer together, despite having been trained on bootstrapped datasets.
- Thompson Samplingis another way to approach the exploration-exploitation problem. Consider the situation where we only have two actions to choose from. We will disregard the context for this example. For each action we have some historical data. By considering the number of wins (α) and losses (β) we can construct beta distributions for each action which can be interpreted as representing a probability distribution of probabilities. Since action A has been attempted fewer times than action B, we see that its distribution is considerably flatter, which represents the uncertainty we have about the reward this action produces. Thus on the one hand we generally want to favor action B over action A, but because we are uncertain about action A, we still want to explore its potential. With Thompson Sampling we dynamically trade off exploration with exploitation by randomly sampling from each posterior distribution and picking the action with the highest sampled probability.
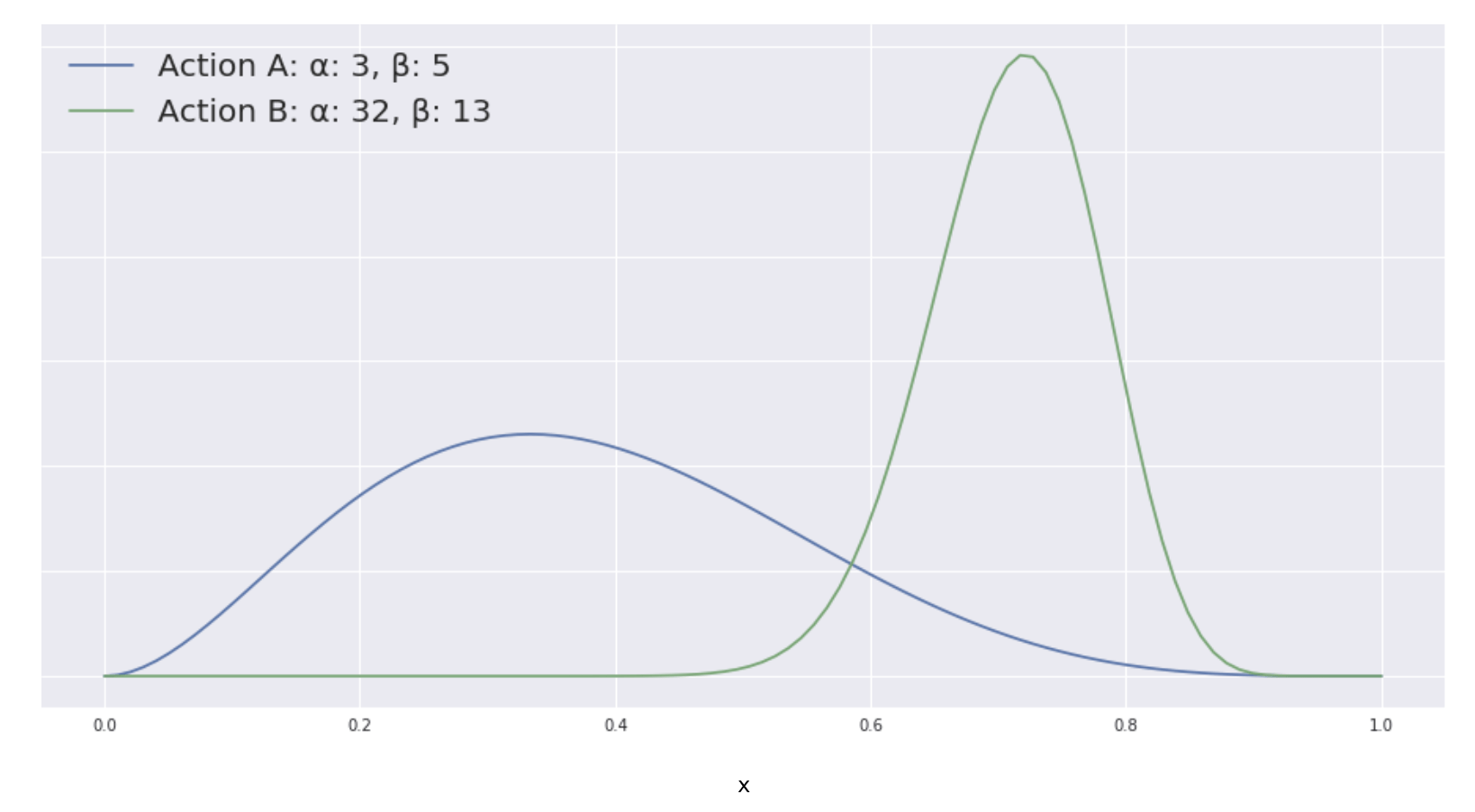
Two beta distributions with different shape parameters.
Let’s look at an actual example from the AutoRescue model. The below example shows the probability of a successful retry by day (the true action space is more granular than this) for a particular set of payment characteristics as returned by our random forest model. Suppose we had a single retry left;in this case, we would opt to retry on penultimate days of the retry window during the epsilon-greedy exploitation stage.
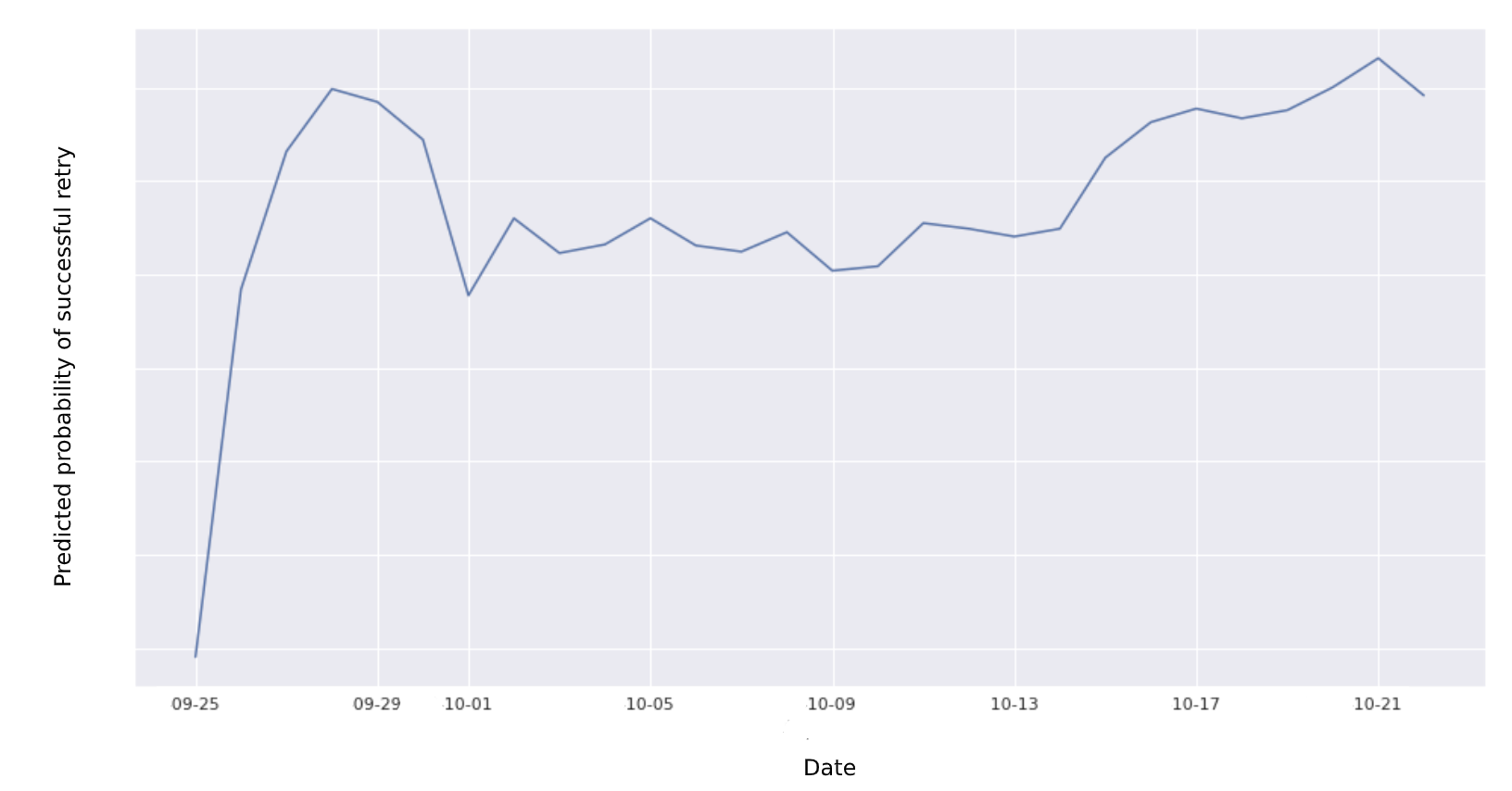
Probabilities returned by random forest model across the retry window.
During the random action selection stage of the epsilon-greedy algorithm, instead of looking at the conditional (weighted) mean usually returned by the random forest, we return the probabilities estimated by the individual trees (pictured below) and randomly select one for each action. We then select the action with the highest sampled probability.
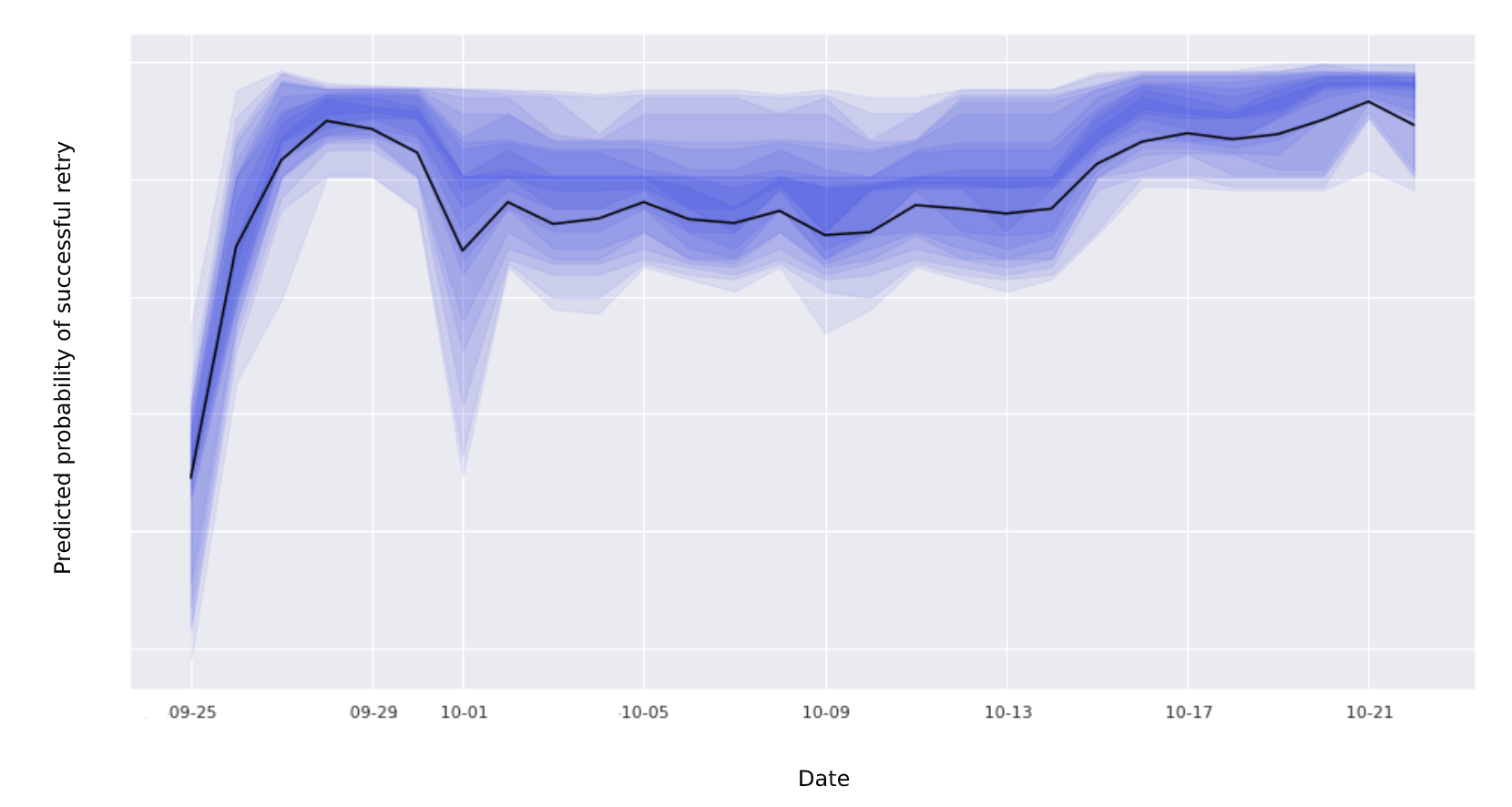
Probabilities returned by the individual trees in the random forest.
As we can see from the above example, our model is more confident about the probability of a successful retry for some actions than others. By allowing the model to still explore areas for which it exhibits a greater degree of uncertainty, we might discover actions that end up returning higher rewards.
Distributing attempts across the retry window
The final problem to solve is how to optimally spread our attempts across the retry window. Looking at the graph above, one might be tempted to schedule a few attempts during the first week and the majority of attempts towards the end of the retry window. However, probabilities for the remaining available actions are recalculated after each failed attempt, leading to a different proposed distribution of attempts across the retry window.
Problems arise when the predicted probability of a retry being successful is high for actions towards the end of the rescue window, but are less so when recalculated after an unsuccessful retry. We noticed that this is particularly the case when certain model input features become dominant, and have a comparable degree of contribution in determining the models output across adjoining actions (we can use SHAP values to quantify this contribution).
We ended up using a heuristic approach in which the model prioritizes(smoothed) local probability peaks. This generally caused the attempts to be spread more across the retry window, and was accompanied by an uplift in successful orders.
Results
An important question still remains: how did this model perform in practice? Over the summer, we conducted an experiment to compare its performance with the baseline strategy we introduced above - namely, retrying each failed payment every four days. The first experiment we tried, which didn’t include logic of distribution attempts throughout the retry window described above, saw our machine learning model convert about 6% more orders than the baseline.
Using these results as a starting point, we spent some time developing the model further, adding the local peaks logic we outlined in the preceding paragraph as well as some additional functionality to improve how the model learns success probabilities from the data it receives. Initial results for this model are even better than those of its previous iteration, and we are confident that we have built a product that can drive real value for our clients.
Technical careers at Adyen
We are on the lookout for talented engineers and technical people to help us build the infrastructure of global commerce!
Check out developer vacancies